PageRank 在 Hadoop 上的实现原理
PageRank 算法的基本思想是，网页的热门程度依赖于指向它的网页的热门程度。假设有页面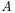 
，有 
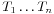这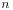 
个页面包含指向 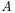的链接，
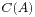代表页面 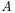所包含的指向别的页面的链接的数量，
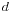是一个介于 0 和 1 之间的常数（成为阻尼系数，一般取 0.85），则页面
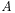的 PR 值（PageRank 值）
![\[ PR(A) = (1-d)+d\left(\frac{PR(T_1)}{C(T_1)}+\dots+\frac{PR(T_n)}{C(T_n)}\right) \]](/user_files/deathspeeder/epics/17272332384e9caa9f78eb1f816ddcdf436a90a0.png "\[ PR(A) = (1-d)+d\left(\frac{PR(T_1)}{C(T_1)}+\dots+\frac{PR(T_n)}{C(T_n)}\right) \]")
这个思想也可以由随即散步模型来解释：即从一随机网页起步，以概率 
跳到另一随机选择的网页， 或以概率 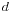随机选择一个当前网页上的链接并跟随此链接。一个网页的 PageRank 就是随机散步者在任意给定时刻访问该网页的概率。被许多网页指向的网页更可能被访问，被具有高 PageRank 的网页指向的网页更可能被访问。
跳到另一随机选择的网页， 或以概率 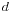随机选择一个当前网页上的链接并跟随此链接。一个网页的 PageRank 就是随机散步者在任意给定时刻访问该网页的概率。被许多网页指向的网页更可能被访问，被具有高 PageRank 的网页指向的网页更可能被访问。
为了求出各个网页的 PR 值，需要对上述方程组进行迭代求解（每个页面的 $PR$ 值都可以根据上述公式得到一个方程），直到方程组的解收敛，或变化的范围很小。在本次实验中，第一次迭代每个页面的初始 PR 值为0.5，当所有页面相邻两次迭代的$PR$值变化小于0.00001时，程序认为函数已经收敛。
实验中的map函数和reduce函数的伪代码如下：
function map
input (PageN, RankN) -> (PageA, PageB, PageC ...)
begin
Nn := the number of outlinks for PageN
for each outlink PageK
TempN = RankN/Nn
output (PageK) -> (PageN, TempN)
output (PageN) -> (PageA, PageB, PageC ...)
end
function reduce
input (PageK) -> (PageN1, TempN1)
(PageK) -> (PageN2, TempN2)
...
(PageK) -> (PageNt, TempNt)
(PageK) -> (PageAk, PageBk, PageCk ...)
begin
TempK := 0
for each inlink PageNi
TempK += TempNi
RankK = 1 + (TempK - 1) * d
output (PageK, RankK) -> (PageAk, PageBk, PageCk ...)
end
function combine
input (PageK) -> (PageN1, TempN1)
(PageK) -> (PageN2, TempN2)
...
(PageK) -> (PageNt, TempNt)
(PageK) -> (PageAk, PageBk, PageCk ...)
begin
TempK := 0
for each inlink PageNi
TempK += TempNi
output (PageK) -> ("", TempK)
if has (PageK) -> (PageAk, PageBk, PageCk ...)
output (PageK) -> (PageAk, PageBk, PageCk ...)
end
在这段伪代码中，reduce函数的输入值（key-value对）的value部分有两种数据结构，即(String, Double)和(List<String>)，在运用hadoop的实现过程中这两个数据结构要作为一个类被写入文件系统。
为了能够判断迭代终止，实现要求能够根据每次迭代的中间输出算出临近两次迭代的PR值变化。其方法是在中间数据结构(PageN, RankN) -> (PageA, PageB, PageC ...)中加入PageN的旧PR值，结构变为(PageN, RankN) -> (OldRankN, PageA, PageB, PageC ...)。这样在每次迭代之间，通过读取迭代的中间文件就可以获得PR值的变化，当所有PR值变化的绝对值小于伐值0.00001时就可以退出迭代了。